Visualizing Bayes’ theorem
I recently came up with what I think is an intuitive way to explain Bayes' Theorem. I searched in google for a while and could not find any article that explains it in this particular way.
Of course there's the wikipedia page, that long article by Yudkowsky, and a bunch of other explanations and tutorials. But none of them have any pictures. So without further ado, and with all the chutzpah I can gather, here goes my explanation.
Probabilities
One of the easiest ways to understand probabilities is to think of them in terms of Venn Diagrams. You basically have a Universe with all the possible outcomes (of an experiment for instance), and you are interested in some subset of them, namely some event. Say we are studying cancer, so we observe people and see whether they have cancer or not. If we take as our Universe all people participating in our study, then there are two possible outcomes for any particular individual, either he has cancer or not. We can then split our universe in two events: the event "people with cancer" (designated as A), and "people with no cancer" (or ~A). We could build a diagram like this:
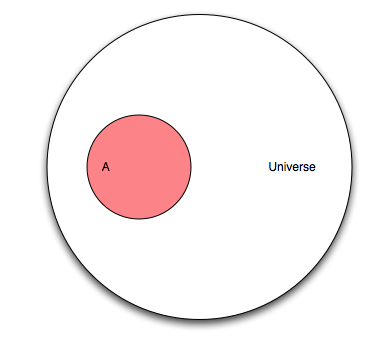
So what is the probability that a randomly chosen person has cancer? It is just the number of elements in A divided by the number of elements of U (the Universe). We denote the number of elements of A as |A|, and read it the cardinality of A. And define the probability of A, P(A), as
Since A can have at most the same number of elements as U, the probability P(A) can be at most one.
Good so far? Okay, let's add another event. Let's say there is a new screening test that is supposed to measure something. That test will be "positive" for some people, and "negative" for some other people. If we take the event B to mean "people for which the test is positive". We can create another diagram:
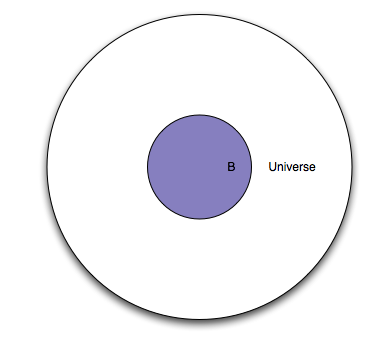
So what is the probability that the test will be "positive" for a randomly selected person? It would be the number of elements of B (cardinality of B, or |B|) divided by the number of elements of U, we call this P(B), the probability of event B occurring.
Note that so far, we have treated the two events in isolation. What happens if we put them together?
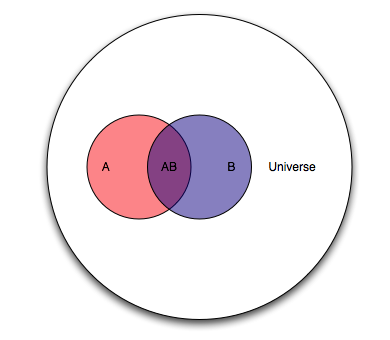
We can compute the probability of both events occurring (AB is a shorthand for A∩B) in the same way.
But this is where it starts to get interesting. What can we read from the diagram above?
We are dealing with an entire Universe (all people), the event A (people with cancer), and the event B (people for whom the test is positive). There is also an overlap now, namely the event AB which we can read as "people with cancer and with a positive test result". There is also the event B - AB or "people without cancer and with a positive test result", and the event A - AB or "people with cancer and with a negative test result".
Now, the question we'd like answered is "given that the test is positive for a randomly selected individual, what is the probability that said individual has cancer?". In terms of our Venn diagram, that translates to "given that we are in region B, what is the probability that we are in region AB?" or stated another way "if we make region B our new Universe, what is the probability of A?". The notation for this is P(A|B) and it is read "the probability of A given B".
So what is it? Well, it should be
And if we divide both the numerator and the denominator by |U|
we can rewrite it using the previously derived equations as
What we've effectively done is change the Universe from U (all people), to B (people for whom the test is positive), but we are still dealing with probabilities defined in U.
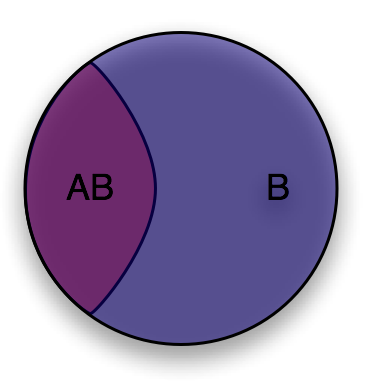
Now let's ask the converse question "given that a randomly selected individual has cancer (event A), what is the probability that the test is positive for that individual (event AB)?". It's easy to see that it is
Now we have everything we need to derive Bayes' theorem, putting those two equations together we get
which is to say P(AB) is the same whether you're looking at it from the point of view of A or B, and finally
Which is Bayes' theorem. I have found that this Venn diagram method lets me re-derive Bayes' theorem at any time without needing to memorize it. It also makes it easier to apply it.
Example
Take the following example from Yudowsky:
1% of women at age forty who participate in routine screening have breast cancer. 80% of women with breast cancer will get positive mammograms. 9.6% of women without breast cancer will also get positive mammograms. A woman in this age group had a positive mammography in a routine screening. What is the probability that she actually has breast cancer?
First of all, let's consider the women with cancer
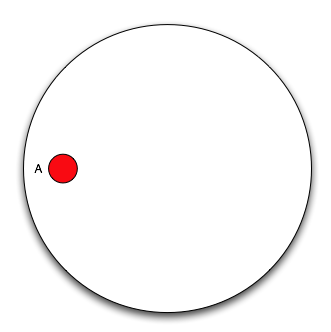
Now add the women with positive mammograms, note that we need to cover 80% of the area of event A and 9.6% of the area outside of event A.
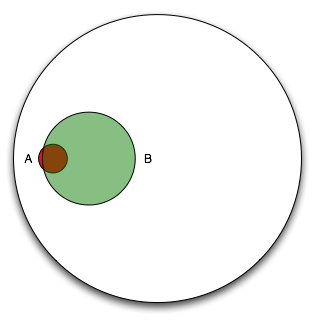
It is clear from the diagram that if we restrict our universe to B (women with positive mammograms), only a small percentage actually have cancer. According to the article, most doctors guessed that the answer to the question was around 80%, which is clearly impossible looking at the diagram!
Note that the efficacy of the test is given from the context of A, "80% of women with breast cancer will get positive mamograms". This can be interpreted as "restricting the universe to just A, what is the probability of B?" or in other words P(B|A).
Even without an exact Venn diagram, visualizing the diagram can help us apply Bayes' theorem:
- 1% of women in the group have breast cancer → P(A) = 0.01
- 80% of those women get a positive mammogram, and 9.6% of the women without breast cancer get a positive mammogram too → P(B) = 0.8 P(A) + 0.096 (1 - P(A)) = 0.008 + 0.09504 = 0.10304
- we can get P(B|A) straight from the problem statement, remember 80% of women with breast cancer get a positive mammogram → P(B|A) = 0.8
Now let's plug those values into Bayes' theorem
which is 0.0776 or about a 7.8% chance of actually having breast cancer given a positive mammogram.
May 1st, 2009 - 13:37
Very well explained! I’ve been reviewing the fundamentals of Bayes theory recently to try to get my head around Bayesian networks from a non stats background. Don’t suppose you could point me in the direction of a similarly visual explanation for that, or maybe consider it in a future post?
May 2nd, 2009 - 10:19
Hm. Bayesian networks… I don’t know of any “visual explanation” of those. I’ll take a look and see if I can come up with something. Thanks for the comment.
May 1st, 2009 - 13:59
Bravo! I actually did the same thing with Venn diagrams to explain it to myself awhile back – I’m glad you took the time to make it clear to others.
May 1st, 2009 - 14:06
How can it be hard to derive Bayes formula if left and right part is essentially the same (A becomes B, B becomes A).
May 2nd, 2009 - 10:21
If I understand your question correctly, you’re saying “what happens when A and B are the same?”. In that case, P(AB) = P(A) = P(B), and P(A|B) = 1. Which is saying “given that event A occurred, what is the probability of event A occurring?”. It should be pretty obvious that it is 1.
May 1st, 2009 - 14:11
http://yudkowsky.net/rational/bayes
May 1st, 2009 - 14:37
This was fantastic. Thank you.
May 1st, 2009 - 15:01
Best explanation of Bayesian, ever, period!!
May 1st, 2009 - 15:14
Great job man! Visualizing this fascinating theorem was a great idea. I dunno though, I always found the actual examples for Bayes’s Theorem to be misleading… I guess that’s just the nature of statistics in odd contexts though!
May 1st, 2009 - 18:31
Dmitriy: Linked in the intro.
Oscar: “Of course there’s the wikipedia page, that long article by Yudkowsky, and a bunch of other explanations and tutorials. But none of them have any pictures.” <– the Java applets/visualizations don’t count as pictures?
May 2nd, 2009 - 10:24
True, the Yudkowsky article has some pictures, and if you keep Java off like I do, all you see are the pictures. My main problem with Yudkowsky’s article is that it’s really, really, really, long! If you are looking to just get the gist of what Bayes’ theorem is saying you are not going to read that much.
May 1st, 2009 - 21:40
Most beautiful and simple explanation. Thanks a lot
May 1st, 2009 - 21:47
Thanks a lot! This was the first time that Bayes actually made sense to me. It’s much easier to understand when visualized.
May 1st, 2009 - 23:41
You are right, memorizing this method gives a hard-to-forget method for rederiving and re-learning Bayes’ rule.
May 2nd, 2009 - 02:33
Thank you for this article!
I really liked the last bit, where you showed the cancer example. That was a good example of “applying the theory shows why you should learn the theory”.
Jens
May 2nd, 2009 - 03:38
Nice. I created something similar a while back due to constantly having to explain this in #math on IRC:
http://imagebin.org/47539
The application to mammograms is a nice one though. Bookmarked!
May 2nd, 2009 - 05:17
This is the absolute best derivation of Bayes theorem I have ever seen, including a course in statistics I did last year. Your post definitely needs to go up on the wikipedia page, under the intuitive reasoning part.
May 2nd, 2009 - 10:58
This is great. Very useful.
I don’t want to be a pedant, and I may be wrong, but aren’t these technically Euler diagrams and not Venn diagrams?
May 2nd, 2009 - 18:05
Well, if you consider the fact that the sets are only defined within the Universe, then they are indeed showing all the possible intersections. Thus they are Venn diagrams.
May 4th, 2009 - 02:59
Wow.
I’ve read quite a few explanations of Bayes’ theorem and this is the first which (in the space of really a few minutes!) has got the point across so succinctly and clearly I now actually understand it.
My thanks.
May 4th, 2009 - 04:44
Brilliant! Thank you!
May 4th, 2009 - 06:58
Thanks a lot!!!
May 4th, 2009 - 10:52
Thank you for re-sparking my love for Discreet Mathematics.
I fondly remember studying this, years ago, but had forgotten the enjoyment of it.
I eagerly await any further of your works.
Perhaps animated…?, perhaps interactive…?
Again Thanks.
May 5th, 2009 - 12:27
This should be made into a visualization app for Google’s new public data search and frankly any data set. Anyone want to work on it with me?
May 5th, 2009 - 14:24
Great job, short, clear and effective – thanks for taking the time to create it!
May 5th, 2009 - 15:34
The exact problem at the end is a good example of how stats can confuse the lay man. Test accuracy should be reported in the rate of false negatives, rather than true positives. The cost of a large number of false negatives can be great relative to a large number of false positives. However, depending on your situation, you could have a lot of false negatives AND false positives, indicating that your test is not well-correlated for the condition being tested for. In fact, just calculating the correlation coefficient is an important step.
May 7th, 2009 - 19:24
Great Job, and excellent example :P | Muy Buen trabajo y excelentes ejemplos!
May 10th, 2009 - 14:18
Great explanation! I teach high school mathematics and am stealing your visualization, example and all, to use in one of my next lessons! :-)
May 28th, 2009 - 15:10
hmm… i think the easiest way to understand bayes theorem is to multiply both sides to get..
P(B) P(A|B) = P(A) P(B|A)
both of these are just P(A intersect B) – probability of A and B is the same as the probability of A times the probability of B given A, or the probability of B times the probability of A given B
May 30th, 2009 - 18:51
David Newman’s book, Hippocrates’ Shadow, Simon&Schuster 2008 has an good treatment of of this in relation to medical interventions and clinical trials. He uses a bar graph variant to demonstrate things Baysean. Good, but not as good as your demonstration! His discussion of this topic sent me to the web where I finally and gratefully got to your visualization! Thanks.
June 5th, 2009 - 00:26
i n really convay to this method of learning of process
June 8th, 2009 - 18:45
this is freagin awesome explanation. thank u :)
June 10th, 2009 - 07:09
I too teach mathematics and am impressed with your clear explaination.
Well done, and thanks for taking the time to lay it out.
June 11th, 2009 - 04:24
An addendum that “completes” the Bayes theorem so that the denominator is the same as in the Yudkowsky article would be nice. Graphically, that would be saying that the area of B is the “union” of two sections: 1. the non-overlap, which is areas in B “starting with” the areas that are NOT in A (the ~A part of the universe) i.e. P(B|~A) * P(~A), 2. the overlap, which is areas in B “starting with” the areas that ARE in A i.e. P(B|A) * P(A). It’s more helpful for applications in which the data makes it easier to figure out probabilities of A and relate those to B, than to figure out probabilities of B.
July 16th, 2009 - 18:48
Professor Oscar,
You are a great prof! You set a benchmark for us trying-to-be’s.
A question. When can I write
P(AB/R) = P(A/R) + P(B/R) ?
What conditions need to be imposed on A, B and R?
Thanks Professor!
Tapan Bagchi at the Indian Institute of Technology Kharagpur
July 19th, 2009 - 03:46
thank you very much…very nice article…
desiNerd,
IITKGP
August 14th, 2009 - 02:23
that’s a really appealing way of expressing Bayes’ theorem
how would the venn-diagram be if the conditional probability of A
didn’t depend on B i.e P(A/B)=P(A) ?
August 14th, 2009 - 12:31
Very nice artice article in every meaning of the word. Have you publised elsewhere?
August 22nd, 2009 - 03:19
Great work dude….I was banging my head to develop intuition on Bayes theorem. Now I got the idea clearly…
Thank u very much..
August 23rd, 2009 - 15:57
May want to check the book by Wonnocott and Wonnocott. They have a visual way of explaining Bayes Theorem
September 16th, 2009 - 10:35
Beautiful explanation. I was searching for something that would help me explain it to undergrads…thanks a bunch.
October 2nd, 2009 - 10:47
This is one of the best explanations I’ve found. Perhaps we can see if I really understand it by trying a real world problem I’m wrestling with.
Here’s the data:
– The odds of a chest pain (CP) being caused by a heart attack is 40%.
– The odds of a CP being caused by other factors (anxiety, depression, etc.) is 60%.
– The odds of a heart attack occurring to a female above age 50 is 80%.
– The odds of a heart attack occurring to a female under age 50 is 20%.
I am presented with a 24 year old female who says she is having chest pain. What is the probability that her chest pain is caused by a heart attack? Is it 0.4 x 0.2 = 0.08?
Also, 78% of patients having heart attacks present with diaphoresis (sweating), so 22% of patients having heart attacks don’t sweat. This female is not sweating, so are the odds of her having a heart attack 0.22 x 0.08 = 0.0176?
Thank you!
October 11th, 2009 - 04:26
You beat me to it! I got the idea of thinking about Bayes’ theorem by Venn diagrams by reading Reza’s An Introduction to Information Theory.
November 26th, 2009 - 15:09
Can someone help me with this question?
One fifth of customers entering a certain Future
Shop store are under 20 years old. 5% of these under 20 year olds make a purchase over $500,
and 10% of the customers 20 years or older make a purchase over $500. What is the probability
that is a major purchase is made, it was by a person 20 years or older?
December 8th, 2009 - 18:58
Just wanted to convey my thanks.
I am teaching this subject to undergrads at a Chinese university and found your explanations and visuals a huge help.
December 13th, 2009 - 18:02
Good visual explanation. I used it to work out a probability but don’t know if the professor is going to reject it.
Thanks.