The Monty Hall Problem
After all the positive feedback I got from Visualizing Bayes' theorem, I thought I’d post my explanation of the Monty Hall problem. I was fascinated for a while with this problem because at first it doesn’t seem to make any sense. And most of the explanations I’ve seen have a magic feel to them. I’ve even seen people with math backgrounds argue against the result.
I think the problem has to do with most of the explanations mixing two very different probability classes. But I’m getting ahead of myself.
The Problem
The problem statement (from Wikipedia) is:
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? (Schrock 1990) [1]
If you are like most people, your gut feeling is going to be “it does not matter. There is a 50-50 chance that the car will be in the door I have already selected”. Like most people, you would be wrong.
In order to solve this problem, you need to consider two very distinct pieces of information. One is “what state is the world in?”, the other is “what events have occurred?”. Let me elaborate.
The States of the world
When I deal with probabilities and get confused, I revert to counting. What are all the possible outcomes? What subset of those outcomes am I looking at? So let’s look at all the posible states.
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats.
Let’s translate that to a simple diagram. We have three doors, let’s label them \(A\), \(B\), and \(C\). We also know that there is a car behind one of the doors, it can be behind door \(A\), \(B\), or \(C\). So we have three possible configurations of the world:
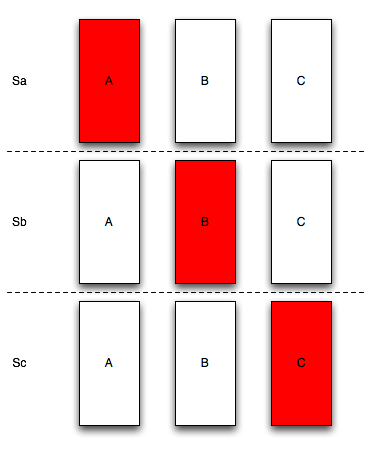
The door with the car has been colored red. The possible states of the world are \(Sa\) (meaning the car is behind door \(A\)), \(Sb\) (car behind door \(B\)), and \(Sc\) (car behind door \(C\)).
Quick, what is the probability of the car being behind door \(A\)? Or to put it another way, what is the probability that the world is in state \(Sa\)? Note that these two questions are the same, but the latter reminds us of the possible states. It is easy then to see that
Now I’m going to ask you a very different question. Assume that instead of playing, you are observing your friend play the game. What is the probability that he will pick door \(A\)? Did you say 1/3? Of course you did, there are three doors and he must pick one. However, and this is really important, these probabilities are completely independent of the probabilities above!
Think of it this way. If two doors had cars behind them instead of just one, would that change the number of states the world can be in? Would it change the probability of your friend choosing door \(A\)? What if all doors had cars? Now there is just a single state for the world, but your friend can still choose door \(A\) with 1/3 probability!
If we now say that \(A\) is the event of your friend opening door \(A\), we can easily see that
which is just saying each door has an equal probability of being opened.
The trick to solving this problem is that you are dealing with two different classes of probabilities. One is the probability that the world is in a given state (a priori), the other is that a participant (you or Monty) chooses any given door. If you can keep these two classes of probabilities separate, you will be able to easily solve this problem.
Let’s see what happens once you have made the choice. Let’s assume you chose the door labeled \(A\).
What does Monty do?
Monty is, of course, the host of the game show. And he is trying to screw you. He doesn’t want you to get the car. He also happens to know where the car is, or in other words, he knows the state of the world. You on the other hand, are only guessing. You chose door \(A\) with probability 1/3, now he gets to choose a door. But there are only two doors left. He must choose either door \(B\) or door \(C\).
So how does Monty choose? What is the probability that Monty will open the door labeled \(B\)? Here’s what the world looks like to Monty:
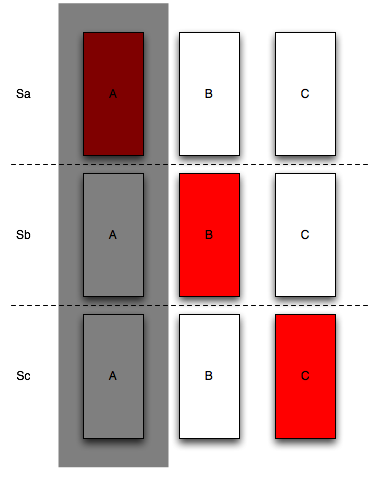
Door A has been chosen, he must choose between doors \(B\) and \(C\). Were he to choose randomly, each door would be equally probable,
The little \(m\)'s are a reminder that this is Monty’s choice, not your original choice. If you wanted to be pedantic you could add \(P(Am) = 0\) since Monty can never choose door \(A\) (you chose that one).
But he knows better than to choose randomly, he knows whether we’re in \(Sa\), \(Sb\), or \(Sc\)! How he chooses will depend on what the state of the world is. If we are in Sa, it doesn’t matter what he chooses, he’ll choose \(B\) or \(C\) with equal probability as neither has a car.[2] That is to say “given that we are in state Sa, Monty chooses door B with probability 1/2”, in other words:
If we are in state Sb, Monty will never choose door \(B\), that would be giving away the prize.
And finally, if we are in state Sc, Monty will always choose door \(B\).
Your turn
And now it’s your turn to make a decision. Do you stay with your original choice of door \(A\)? Or do you switch and choose door \(C\)?
First of all, does it matter? Is there any difference whether we switch or not? The answer is a resounding YES! Monty gave away information about the state of the world by choosing door \(B\). We can use that information.
What we are really trying to figure out is this: “what configuration is the world in?” Monty knows, he used that information to choose door \(B\). Now we have to ask ourselves, “given that Monty chose door \(B\), what is the probability that the world is in state \(Sa\) versus the probability of the world being in state \(Sc\)?” Note that we have eliminated \(Sb\) because Monty has already opened door B and there was no car!
Here is where we can apply Bayes' formula to get an answer:
and plugging in the values we have already computed:
Which means we have a 1/3 chance the car is behind our original choice of door \(A\). Note that this 1/3 probability is different than the original \(P(A) = 1/3\) we had computed. It ends up being the same number, but it is really a different probability!
What about the car being behind door \(C\)? What is the probability that we are in state \(Sc\), given that Monty chose door \(B\)?
and plugging in the values we get:
Which means we have a 2/3 chance the car is behind the other door (door \(C\)). Therefore we should switch.
Does it matter if Monty knows?
The only reason we managed to gain any information from Monty’s choice of door \(B\) is that he knows the state of the world and acts differently depending on what state is the correct one. If Monty didn’t know, he would have been choosing randomly between doors \(B\) and \(C\) and we would not have gained any information (except that \(Sb\) is not possible since there was no car behind door \(B\)).
If Monty always chooses door \(B\) when neither \(B\) nor \(C\) have the car, we would not have gained any information when he opens door \(B\), but we would gain information if he opens door \(C\) (do you see why?).
Note that it is still to our advantage to switch doors, since in this case the probabilities for the states \(Sa\) and \(Sc\) are the same (1/2). And if we don’t know whether Monty knows or not, we might get an advantage from switching.
 Oscar Bonilla
Oscar Bonilla